|
Bruno
de Finetti: così è, se vi pare - 2
“.....ma davvero esiste la
probabilità? e cosa mai sarebbe? Io risponderei di no, che non esiste.”
(Luca Nicotra) - Le definizioni di probabilità classica,
frequentista e assiomatica.
 Diceva
il matematico e filosofo americano Charles Sanders Pierce: “Questa
branca della matematica, la probabilità, è la sola, credo, in cui anche
validi autori hanno dato spesso risultati erronei”. E ancora
Bertrand Russell: “Il concetto di probabilità è il più importante
della scienza moderna, soprattutto perché nessuno ha la più pallida idea
del suo significato”. Queste affermazioni mostrano in maniera molto
incisiva che il terreno delle argomentazioni sulla probabilità è stato,
e forse ancora è, molto “scivoloso”; purtroppo, ancor oggi, è
possibile leggere vari sproloqui sulla probabilità, mascherati da quel
mitico rigore matematico, cui sempre ci si appella, anche
ingiustificatamente, per dar consistenza alle nostre argomentazioni.
Le definizioni che illustreremo si riferiscono tutte ad eventi semplici.
La prima definizione matematica di probabilità, e per questo motivo detta
“classica1”,
è la seguente: “La probabilità è il rapporto fra il numero di
eventi favorevoli e il numero di eventi possibili, essendo quest’ultimi
tutti equiprobabili”. Ovviamente l’aggettivo “favorevole” non
è riferito al contenuto dell’evento, bensì alla nostra attesa che esso
si realizzi: favorevole è semplicemente l’evento su cui fissiamo
l’attenzione, che ci attendiamo che si realizzi o sia vero, di cui
vogliamo valutare numericamente (con la probabilità) la possibilità di
accadere o di essere vero, indipendentemente dal fatto che sia o no un
evento piacevole o vantaggioso. Essa, a volte, è detta anche
“definizione per partizione”, poiché implica una partizione
dell’insieme di tutti gli eventi possibili nei due sottoinsiemi degli
eventi favorevoli e degli eventi non-favorevoli. Questa definizione ha un
dominio di applicazione limitato da due condizioni: 1) è applicabile
soltanto in tutti i casi in cui è possibile conoscere quali e quanti sono
gli eventi che si possono realizzare e quali e quanti sono quelli
favorevoli; 2) gli eventi possibili devono avere tutti la stessa
probabilità, vale a dire non ci deve essere nessun motivo che favorisca
la realizzazione dell’uno piuttosto che dell’altro.
Il classico esempio di applicazione di questa definizione è il lancio di
una moneta, perfettamente “equilibrata” o “simmetrica”, nel senso
che non ci sia maggior concentrazione di massa su una faccia piuttosto che
sull’altra; gli eventi possibili sono due (testa, croce)2,
mutuamente escludentesi, mentre l’evento favorevole è uno dei due (o
testa o croce). La probabilità che in un lancio la moneta cada
presentando croce è quindi ½ e ugualmente ½ è la probabilità che la
moneta cada presentando testa.
La presenza dell’aggettivo “equiprobabile” rende difettosa questa
definizione dal punto di vista logico, chiudendola in un circolo vizioso,
poiché essa fa uso dello stesso concetto (la probabilità) che intende
definire.
 Osservava
Henry Poincarè (La scienza e l’ipotesi):
“. . . Siamo costretti a definire il probabile dal probabile. Come
possiamo sapere se due casi sono ugualmente probabili? Sarà per
convenzione?”. Usualmente, tale anomalia è superata ricorrendo al
Principio della Ragion Non Sufficiente o Principio d’Indifferenza3,
introdotto da Pierre Simon de Laplace, per il quale gli eventi vanno
intesi come equiprobabili se non c’è nessuna ragione per credere il
contrario, in quanto si presume che vi sia simmetria perfetta rispetto ai
casi possibili. Ma è chiaro che anche una siffatta giustificazione non è
del tutto soddisfacente e attira facilmente critiche ben fondate! Il fatto
di non essere in grado di formulare ragioni in contrario non esclude che
in realtà vi siano.
La definizione classica di probabilità presuppone la possibilità di
eseguire “virtualmente”, e non materialmente, l’esperimento o prova
che può dar luogo all’evento atteso, individuando tutti i possibili
esiti, e fra questi quelli in cui si presenta l’evento in
considerazione, dal semplice esame dell’oggetto protagonista
dell’evento: il lancio di un dado può essere facilmente immaginato e
con esso i suoi possibili risultati, eventi croce o testa, anche senza
materialmente effettuare l’esperimento, perché l’esame dell’oggetto
“dado” ci consente di sapere quali essi sono. Ma tale possibilità
riguarda soltanto un limitato sottoinsieme dell’universo di tutti i casi
reali, nella maggior parte dei quali, invece, non è applicabile.
In molte situazioni reali, infatti, l’evento di cui vogliamo calcolare
la probabilità non può essere generato da un esperimento virtuale, ma,
al contrario, può manifestarsi soltanto “a posteriori”, con
l’esperienza effettiva. Occorre, dunque, compiere materialmente gli
esperimenti che generano l’evento. Utilizzando i risultati ottenuti,
viene spontaneo calcolare il rapporto fra il numero di esiti positivi
dell’esperimento (quelli in cui si presenta l’evento atteso) e il
numero totale delle prove, cioè la frequenza relativa dell’evento,
rapporto che caratterizza bene la “presenza” di questo nella totalità
degli esperimenti compiuti. In situazioni di questo tipo si è tentati di
identificare i casi favorevoli con gli esiti positivi delle prove, e i
casi possibili con le prove effettuate, riproponendo l’applicazione
della definizione classica, però con una sostanziale differenza rispetto
alle situazioni cui quest’ultima è applicabile: ora infatti i casi
possibili sarebbero “soltanto” le prove finora effettuate, che non
esauriscono tutte quelle effettuabili, che sono infinite, e analogamente i
casi favorevoli sarebbero “soltanto” gli esperimenti finora effettuati
che hanno generato l’evento atteso. In altre parole, nella definizione
classica di probabilità gli eventi favorevoli e possibili sono
“tutti” quelli che effettivamente sono favorevoli e possibili; nelle
nuove situazioni investigate, invece, essi sono quelli “finora
esperiti” e quindi risultano variabili secondo il numero di prove
effettuate, che è necessariamente una scelta dello sperimentatore.
Qualunque sia il numero di esperimenti da questi deciso, le prove non
ancora fatte, ma fattibili, costituiscono altrettanti casi possibili, fra
i quali potranno esserci altri casi favorevoli. Pertanto, se assumessimo
“tout court” come probabilità la frequenza relativa dell’evento,
avremmo una probabilità variabile perché dipendente dal numero di
esperimenti effettuati, che è variabile, contrariamente all’unicità
del valore calcolato con la definizione classica. Ciò che possiamo
investigare è, invece, se esistono condizioni che autorizzano tale
assunzione entro un grado di approssimazione accettabile, consapevoli
quindi che con tale assunzione dovremmo accontentarci di un valore
“approssimativo” di probabilità, che non può essere rigorosamente
unico come nella definizione classica.
A tale scopo, occorre prendere in considerazione i casi in cui è
calcolabile la probabilità per partizione, effettuando “realmente” un
certo numero di prove. Consideriamo il solito lancio di una moneta.
Ebbene, effettuando più lanci della moneta, “cercando” di mantenere
inalterate le condizioni sotto cui essi avvengono, si può osservare che
all’aumentare del loro numero, la frequenza relativa dell’evento
“croce” (e lo stesso vale per l’evento complementare “testa”)
tende a stabilizzarsi attorno a un valore molto prossimo alla probabilità
(0,5 o 50%) calcolata con la definizione classica. Tale tipo di
esperimento si può ripetere in tutti i casi ai quali è applicabile
quest’ultima. Eseguendo successive serie di esperimenti, in ciascuna
delle quali si aumenta progressivamente il numero di esperimenti rispetto
alla serie precedente, si osserva che all’aumentare del numero di
questi, il valore della frequenza relativa dell’evento considerato tende
a stabilizzarsi attorno a uno stesso valore: è la cosiddetta “legge
empirica del caso” o “legge empirica dei grandi numeri”. Tale legge,
spesso, erroneamente è confusa con il teorema di Bernoulli : lim P {
|(n/N) - p| < e } = 1 per N ’:, che
asserisce semplicemente che aumentando indefinitamente il numero N di
prove, tende alla certezza (P = 1) la probabilità che la frequenza
relativa dell’evento scarti dalla probabilità (classica) p per meno di
un numero positivo å comunque piccolo. Questo teorema, qualche volta,
viene erroneamente utilizzato come anello di congiunzione fra le
definizioni classica e frequentista di probabilità, come è stato
acutamente criticato da Bruno de Finetti: “non si sfugge al dilemma
che la stessa cosa non si può assumere prima per definizione e poi
dimostrare come teorema, né alla contraddizione di una definizione che
assumerebbe una cosa certa mentre il teorema afferma che è soltanto molto
probabile”. L’unico anello di congiunzione plausibile fra
probabilità per partizione e frequenza relativa è invece la semplice e
più onesta legge empirica del caso, in virtù della quale risulta
“plausibile” ribaltare i termini dell’osservazione sperimentale, e
“assumere” come probabilità la frequenza relativa dell’evento
determinata per un numero “abbastanza grande” di esperimenti, in tutti
quei casi in cui è possibile “ripetere a pari condizioni”
l’esperimento. È questo valore limite, nel senso non matematico ma
sperimentale sopra evidenziato, che viene assunto come valore della
probabilità nella definizione frequentista. Esso, non essendo un
“limite” in senso matematico, non è determinabile tramite operazioni
matematiche, bensì tramite un numero teoricamente infinito di
esperimenti, in aperto contrasto con il modo operativo sperimentale che
conosce soltanto il “finito”, per cui in pratica è determinabile con
un “opportuno” numero finito di esperimenti.
Secondo la definizione “frequentista4”
, dunque, “ la probabilità di un evento è il rapporto fra il numero
di esperimenti in cui esso si è verificato e il numero totale di
esperimenti eseguiti nelle stesse condizioni, essendo tale numero
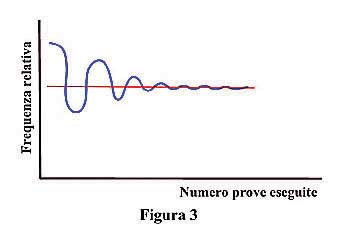
opportunamente grande”. Quale
debba essere in pratica tale numero non è determinabile a priori, ma è
lo sperimentatore che deve definirlo, in base alla legge empirica dei
grandi numeri, che lo autorizza a porre fine all’esecuzione degli
esperimenti quando rileva che la frequenza relativa dell’evento presenta
oscillazioni sempre più piccole: il valore medio di queste è assunto
come valore della probabilità (figura 3). E tale decisione non può che
essere soggettiva, approssimativa e variabile da sperimentatore a
sperimentatore e, anche per uno stesso sperimentatore, ancora variabile da
una serie di esperimenti all’altra (perché, per esempio, non è mai
possibile mantenere perfettamente identiche le condizioni sotto cui
avviene la prova, per cui il numero di esperimenti oltre il quale le
oscillazioni della frequenza relativa diventano “sempre più piccole”
cambierà per lo stesso sperimentatore da una serie di esperimenti
all’altra). La probabilità, in tale definizione, dipende dunque non
soltanto dal numero di esperimenti fatti ma anche dalla valutazione di
identità delle condizioni operative, per cui non è univocamente
determinabile ed è affetta da errore sperimentale, come la misura di una
qualunque altra grandezza fisica.
(continua)
Note:
1 Formulata nel 1812 dal
matematico francese Pierre Simon de Laplace (Théorie analytique des
probabilités).
2 Si esclude il caso, che in
realtà potrebbe verificarsi, che la moneta cada di taglio, senza
presentare quindi nè testa nè croce.
3 Da non confondersi con il
Principio di Ragion Sufficiente di Leibnitz, secondo il quale “nulla
accade senza che vi sia ragione perché accada proprio così invece che
altrimenti”
4 Proposta da Richard von Mises
e Hans Reichenbach agli inizi del secolo XX.
|
