Anno IX numero 9 - settembre 2000

 CURIOSITÀ STORICHE

Voglia di calcolare
Breve storia degli strumenti

di Luca Nicotra

Fin dall'antichità, l'homo sapiens ha sentito la necessità di creare strumenti che lo assistessero nelle sue varie attività. In particolare, una gran rilevanza e diffusione hanno 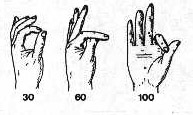sempre avuto gli strumenti per calcolare, dai primi rudimentali abachi in uso presso le più antiche civiltà fino agli attuali calcolatori elettronici. Nelle varie puntate ricostruiremo brevemente la storia di tali strumenti, mostrando anche alcune curiosità, come l'impropria attribuzione a Pitagora dell'omonima tavola di moltiplicazione e alcune sue semplici ma curiose proprietà.

La mano: primo strumento
La mano ha costituito, e costituisce tutt'oggi, lo strumento più semplice e naturale d'aiuto all'uomo per svariati compiti, materiali e no. Con la mano egli è in grado di vestirsi, mangiare, bere, eseguire sforzi fisici, salutare, minacciare, parlare attraverso un linguaggio gestuale. Non sorprende dunque che l'uomo, anche per contare e far di conto, prima ancora di costruire altri strumenti, abbia sfruttato le straordinarie possibilità delle sue mani. "Certo, –dice Georges Ifrah, insigne esperto di numerologia– per l'alto numero delle sue parti ossee e delle articolazioni corrispondenti, per la disposizione asimmetrica delle dita e la loro relativa autonomia, infine, per il dialogo permanente che essa intrattiene col cervello, la mano dell'uomo costituisce la più straordinaria concentrazione naturale di risorse in questo campo" [1].
Le possibilità offerte dalle mani per contare sono svariate e furono utilizzate dai popoli antichi, dall'Estremo Oriente fino al Mediterraneo.
La maniera più banale è quella di rappresentare con le dita i numeri interi a cominciare dall'unità, come si fa con i bambini per insegnare loro a contare. Si tenga presente che il termine 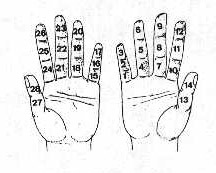anglosassone digit, ormai entrato nell'uso universale per indicare il concetto di cifra, deriva dal latino digitus, che significa dito.
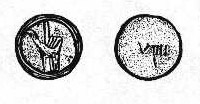
Un metodo, molto diffuso nell'Antico Impero dell'Egitto faraonico e nell'Impero Romano, era basato su ben definite gestualità delle mani, simili al linguaggio dei sordomuti, che permetteva di contare fino a 99 su una mano e fino a 9.999 su entrambe le mani (figura 1). Gli scavi archeologici hanno portato alla luce molti gettoni romani di osso o avorio che portano una doppia rappresentazione dei numeri: su una faccia la rappresentazione tramite le mani e sull'altra il numerale romano (figura 2).
Un'altra tecnica, tutt'oggi diffusa in India e nella Cina meridionale, consisteva nel contare per mezzo 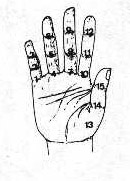delle 14 falangi (figura 3) o delle 15 giunture delle dita di ciascuna mano (figura 4). Il "grassello" del pollice contava come giuntura.
I Cinesi estesero notevolmente le possibilità di rappresentazione dei numeri tramite le mani, considerando ciascuna giuntura delle dita suddivisa in tre parti: sinistra, centro e destra. Introdussero, poi, a livello soltanto strumentale, il principio posizionale nella numerazione. Ogni dito, infatti, rappresentava un ordine di unità. Nel sistema decimale, cominciando dalla mano destra, il mignolo stava per le unità semplici, l'anulare per le decine, il medio per le centinaia ecc., proseguendo la numerazione, con lo stesso criterio, 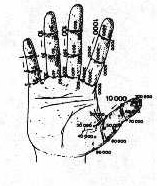nella mano sinistra. Le parti sinistra, centrale e destra delle tre articolazioni delle dita rappresentavano le unità semplici, per un totale di nove, come vuole il sistema di numerazione decimale. In conclusione, con una mano si arrivava a rappresentare fino al numero 99.999 e con entrambe le mani si poteva arrivare fino al numero 9.999.999.999 (figura 5). Con tale sistema, oltre che contare, si era in grado di eseguire tutte le operazioni aritmetiche fino allora conosciute.

L'abaco
La costruzione di strumenti 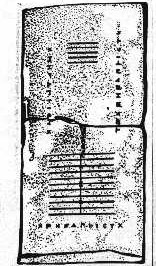per computare è comune a tutti i popoli dell'antichità. Essi sono stati utilizzati anche dopo l'introduzione dei sistemi di numerazione scritta, sia perché il calcolo strumentale è più rapido, sia perché fino a tempi abbastanza recenti erano veramente poche le persone che sapevano leggere, e quindi in grado di utilizzare la numerazione scritta.
I primi a costruire un abaco furono, allo stato attuale delle fonti storiche disponibili, i Babilonesi, che intorno al V, IV sec. a.C. utilizzavano già uno strumento di marmo di forma rettangolare, su cui erano incisi due gruppi di undici linee verticali attraversate da una linea orizzontale. Nell'isola di Salamina, è stato ritrovato un esemplare di tale abaco (figura 6).

L'abaco a polvere
Gli antichi Fenici, gli Ebrei e poi i Greci, gli Etruschi e i Romani usavano come strumento di computazione una tavoletta rettangolare di legno o una lamina di bronzo, chiamata abak dai Fenici, avak dagli Ebrei, abac dai Greci, apcar dagli Etruschi, abacus dai Romani. Il significato comune a tutti i termini è quello dell'antica parola fenicia abak (polvere), dalla quale derivano. Infatti, sulla tavoletta aderiva, per mezzo di un collante, della polvere di colore verde (pulvis hyalinus) in modo che su di essa si potessero tracciare con una bacchetta (radius) simboli numerici e figure geometriche, utilizzandola così come noi oggi usiamo la lavagna.
L'abaco a polvere è menzionato da numerosi autori antichi. Cicerone (106-43 a.C.) ne parla nelle sue Tuscolanae Disputationes (Quaestio V,23):
" … ex eadem urbe humilem homunculum a pulvere et radio excitabo, qui multis annis post fuit Archimedes",
da cui risulta, com'è a tutti noto, che Archimede usava tale tipo di abaco, per disegnare figure geometriche.
Anche Virgilio (70-19 d.C.) lo cita nelle sue Egloghe (III,40):
" … si quis fuit alter
Descripsit radio totum qui gentibus orbem".
Persio (34-62 d.C.) scrive nella Satira I:
"Nec qui abaco numeros et secto in pulvere metas,
Scit risisse vafer, multum gaudere paratus.
Si cynico barbam petulans nonaria vellat."
Marziano Capella (sec. V d.C.) nella sua enciclopedia sulle sette arti libertali De Nuptiis Philologiae et Mercuri, scritta in forma allegorica, lo descrive ampiamente nei libri dedicati alla Geometria e all'Aritmetica:
"Patent denique jam ingressurae artes quae decentem quamdam, atque hyalini pulveris respersione coloratam velut mensulam gestitantes. Illud quippe quod gerulae detulerunt, abacus nuncupatur, res depingendis designandisque opportuna formis. Quippe ubi vel lineares ductus, vel circulares flexus, vel triangulares abraduntur aufractus" (Liber VI, De Geometria).
"Sic abacum perstare jubet, sic tegmine glauco pandere pulvereum formarum ductibus aequor." (Liber VII, De Arithmetica).

L'abaco a lapilli
Successivamente, i Romani usarono un altro tipo di abaco, costituito da una tavoletta rettangolare sulla quale erano praticate alcune scanalature parallele al lato minore, al di sopra di ciascuna delle quali si trovavano impresse le lettere del sistema di numerazione romano, che indicavano l'ordine delle unità al quale la scanalatura era riservata. Cominciando da destra, la prima scanalatura era quella delle unità frazionarie, la seconda era dedicata alle unità semplici e sopra di essa figurava il numerale I, la terza era dedicata alle decine e aveva sovraimpresso il numerale X, la quarta scanalatura era quella delle centinaia e aveva il corrispondente numerale C, e così via. All'interno di ciascuna scanalatura, secondo i modelli di abaco che si susseguirono nel tempo, erano disposti tanti sassolini (calculi, da cui il termine calcolare) o dischetti (abaculi) o monetine (denarii supputatorii) quanti erano le unità di quell'ordine da rappresentare. Se in corrispondenza di ciascuna scanalatura, iniziando dalla prima a sinistra non vuota, si scrive il numerale corrispondente all'ordine delle unità della scanalatura tante volte quanti sono i calculi in essa contenuta, si ottiene la rappresentazione scritta del numero indicato dall'abaco, secondo il sistema di numerazione additivo romano1. Il numero era, quindi, pensato come somma delle unità dei vari ordini. Di tale abaco, utilizzato dai Greci e dai Romani, esistono numerose citazioni nella letteratura classica (Polibio, Plutarco, Erodoto, Lisia, Orazio). Basti ricordare quella di Orazio, il quale nella Satira I, 6, descrive i fanciulli che si recano a scuola portando a tracolla la tavoletta e la cassettina contenente i calculi:
"Causa fuit pater bis, qui macro pauper agello
Noluit in Flavi ludum me mittere, magni
Quopueri magnis e centurionibus orti,
Laevo suspensi loculos tabulamque lacerto,
Ibant octonis referentes idibus aera."
Come fossero eseguiti i calcoli con l'abaco a lapilli, com'è anche chiamato il tipo d'abaco precedentemente descritto, non è stato tramandato ed è perciò sostanzialmente sconosciuto, anche se sono state avanzate varie congetture. Ciò che è certo è che il suo uso doveva essere semplice e rapido, essendo esso usato dai ceti non colti e dai ragazzi a scuola, come ci racconta Orazio. Dell'abaco a lapilli sono pervenute fino a noi due testimonianze iconografiche: un'effigie incisa nella gemma calculatoria conservata al gabinetto delle medaglie della Biblioteca Nazionale di Parigi e un'altra scolpita in un sarcofago romano conservato al Museo Capitolino di Roma. Nella gemma calcolatoria di Parigi è rappresentato un ragazzo seduto davanti a un tripode contenente i calculi e che regge con la mano sinistra la tavola2. Nel sarcofago romano, invece, è rappresentato uno schiavo che tiene fra le mani una tavoletta con dei sassolini3.
L'uso dell'abaco a lapilli (figura 7) si protrasse fino all'inizio del sec. XVI, com'è testimoniato dallo scolio a Beda il Venerabile del Noviomago (Scholia in Bedam, cap. De Digitatione):
"Est et alia numerorum ratio per calculos, in tabula delineata, ductibus parallelispositos quae et ipsa vetus est, neque ab usu recessit: nisi quod loco calculorum, nummie nunc utantur, atque hujus est et fuit usus in numerandis speciebus negotialibus."

L'abaco a bottoni
In una lettera inviata al Lipsio, il 15 marzo 1593, e in una successiva inviata al Camerario, il 18 agosto dello stesso anno, il Velsero descrisse un terzo tipo di abaco usato dai 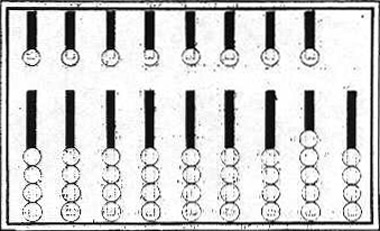Romani, detto "abaco a bottoni"4. Nel 1853, il padre gesuita Garrucci trovò un esemplare di abaco a bottoni che oggi definiremmo di formato tascabile, e che fu poi conservato al museo Kircheriano5 . Si tratta di una lamina di bronzo, lunga 11,5 cm e larga 9,4 cm, recante nove scanalature parallele al lato minore divise in due parti da una linea orizzontale (figura 8). Ciascuna scanalatura della parte inferiore contiene quattro bottoni (aerae), ad eccezione della seconda da destra che ne ha cinque. Le scanalature superiori hanno invece ciascuna un solo bottone, che vale cinque unità dell'ordine della scanalatura cui appartiene. Iniziando da destra, le prime due scanalature sono dedicate alla rappresentazione delle unità frazionarie: la prima, priva della parte superiore, è dedicata alla semioncia S (semis), al quarto d'oncia É (sicilicus), e al sesto d'oncia Z (sextula), mentre la seconda è riservata alle once. Le successive scanalature dell'abaco sono dedicate rispettivamente alle unità semplici I, alle decine X, alle centinaia C, alle migliaia (I) , alle decine di migliaia ((I)), alle centinaia di migliaia (((I))), ai milioni ((((I))))6. La rappresentazione di un numero era effettuata spostando entro ciascuna scanalatura, verso la linea di separazione fra le due parti dell'abaco, un numero di bottoni pari al numero di unità da rappresentare per ciascun ordine, tenendo presente che un bottone superiore vale cinque unità dello stesso ordine. Per esempio, il numero otto era rappresentato spostando, nella terza scanalatura delle unità semplici, verso la linea orizzontale tre bottoni inferiori e quello superiore.
L'uso dell'abaco a bottoni venne meno già nel secolo XIV, vale a dire due secoli prima rispetto all'abbandono dell'abaco a lapilli, probabilmente per la ragione che essendo più complicato di quello a lapilli, era utilizzato soprattutto dai ceti più abbienti, i quali vennero per primi a conoscenza sia del nuovo abaco a colonne sia del nuovo sistema posizionale di numerazione scritta. Questo utilizzava le cifre indoarabiche diffuse nell'Occidente europeo nel secolo XIII, principalmente per opera di Leonardo Pisano detto Fibonacci, che nel suo celeberrimo Liber Abaci (1202) non solo illustrò il nuovo sistema, ma espose anche, utilizzandolo, tutta l'aritmetica elementare allora nota. Probabilmente, la diffusione in Europa del sistema posizionale e delle cifre indoarabiche avvenne gradualmente attraverso gl'intensi contatti commerciali dei ricchi mercanti italiani con il mondo orientale, particolarmente fiorenti nel Basso Medioevo (secoli XI-XIII). Tali mercanti conoscevano, per motivi di contabilità commerciale, il modo di calcolare basato sul principio di posizione e sulle cifre indiane, già in uso in oriente. In ogni caso, si tenga presente che nel 1156 appariva nel Mondo Occidentale la prima traduzione in latino, con il titolo Liber algorismi de numero indorum, dell'opera scritta negli anni 800-825 dal matematico arabo Mohammed Ben Musa detto Al Khovarizmi, nella quale è illustrato il sistema di numerazione posizionale usato dagli Indiani già dal secolo V. Tuttavia, il merito della diffusione di tale sistema in Occidente è dovuto all'opera citata di Leonardo Pisano, che ebbe gran diffusione e influenza in Europa.

L'abaco ad anelli
Si ritiene che i primi Cristiani diffusero in Cina l'abaco nel secolo XIII circa, almeno nella forma attuale dello swan-pan (figura 10), come è chiamato l'abaco dai cinesi. Questa tesi è confortata dalla notevole rassomiglianza fra lo swan-pan e l'abaco tascabile dei Romani: al posto delle scanalature ci sono delle aste verticali, e al posto dei bottoni delle palline che possono scorrere lungo tali aste. In particolare, come nell'abaco a bottoni romano, l'abaco cinese è diviso verticalmente in due parti da un'asticciola orizzontale, e per ogni asta ci sono due palline superiori e cinque inferiori. Ogni asta, come nell'abaco romano, corrisponde a un ordine decimale, e spesso le prime due da destra sono dedicate rispettivamente ai centesimi e ai decimi, per cui l'ordine delle unità corrisponde alla terza asta, quello delle decine alla quarta, e così via. Il numero di unità di ogni ordine è ottenuto spostando verso la traversa orizzontale il numero di palline necessarie, tenendo presente che ogni pallina della parte superiore vale cinque unità dell'ordine corrispondente all'asta entro cui è infilata. In tal modo, sembrerebbe che lo swan-pan possieda per ogni asta due palline in più rispetto al necessario, una superiore e una inferiore, poiché per rappresentare il numero massimo di unità di ciascun ordine, cioè nove, è sufficiente spostare verso la traversa di separazione una pallina superiore, che vale 5, e quattro inferiori, che valgono 4. In realtà le due palline in eccedenza servono per rappresentare risultati 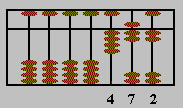parziali di addizioni, sottrazioni, moltiplicazioni e divisioni, superiori a nove. Nel 1930 i giapponesi modificarono l'abaco cinese dall'originario modello 2/5 nel modello 1/4,7 ottenendo il loro soroban (figura 11), tutt'oggi in uso in Giappone presso i negozi e insegnato nelle scuole. I cinesi e i giapponesi erano molto abili nel calcolo strumentale e ancor oggi la cultura dell'abaco è molto diffusa in Cina e in Giappone. Il 12 novembre 1946, cioè agli albori dei calcolatori elettronici, a Tokyo si tenne una curiosa competizione sportiva di velocità fra un operatore di calcolatrice elettrica e un abachista, con un risultato davvero incredibile: la palma della vittoria spettò all'abachista!

La Mensa Pithagorica. Dall'abaco all'algoritmo
L'osservazione attenta dell'abaco suggerisce in quale modo, probabilmente, avvenne il passaggio dall'antico abaco romano alla sua versione medioevale, l'"abaco a colonne", che risulta ormai uno strumento di calcolo in perfetta sintonia con il sistema posizionale di numerazione scritta, tanto da perdere la sua ragion d'essere.
Infatti, l'abaco descritto 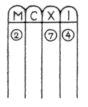precedentemente, nelle sue varie forme costruttive, contiene esso stesso l'idea del valore posizionale delle cifre, in quanto ogni scanalatura è dedicata a un ordine di unità e quindi pone in evidenza il diverso peso dei calculi secondo la scanalatura cui appartengono. Per esempio, tre calculi entro la scanalatura delle unità semplici hanno evidentemente un valore diverso (tre unità semplici) da quello di altrettanti calculi contenuti nella scanalatura delle centinaia (tre centinaia). Insomma, la rappresentazione di un numero fornita dall'abaco (rappresentazione strumentale) era decisamente posizionale fin da tempi antichissimi, mentre quella scritta (rappresentazione per numerali) era additiva. Ebbene, l'applicazione del principio di economia alla rappresentazione dei numeri per mezzo dell'abaco portò a trasferire il principio di posizione anche alla scrittura.
Per intendere pienamente il significato di questa asserzione, conviene esaminare più a fondo l'idea che sta alla base del principio di posizione.
Il sistema utilizzato per numerare si basava, già da tempi remoti, sulla possibilità di pensare un numero come somma delle sue unità semplici raggruppate in gruppi di potenze della base del sistema di numerazione adottato. In particolare, nel sistema di numerazione decimale, che è a base dieci, i successivi gruppi contengono tante unità semplici quante ne indicano le successive potenze naturali del numero dieci. In altri termini, un numero qualsiasi è considerato come somma di gruppi di 100=1, 101=10, 102=100, 103=1000 unità ecc. Tali gruppi, a loro volta, sono considerati essi stessi unità complesse, rispettivamente del primo ordine o semplici, del secondo ordine o decine, del terzo ordine o centinaia, del quarto ordine o migliaia ecc. In tal modo, nel sistema decimale, dieci unità di un certo ordine formano un'unità dell'ordine immediatamente superiore. Per rappresentare un numero, sarebbe quindi necessario un doppio sistema di rappresentazione: un insieme infinito di simboli per le unità dei vari ordini superiori al primo (nel sistema decimale le decine, centinaia ecc.) e un insieme finito di simboli per rappresentare il numero di unità di ciascun ordine che per definizione è, al massimo, pari alla base meno uno ( nove, nel sistema di numerazione decimale).
Ora, è interessante osservare che tali simboli possono essere sia oggetti che segni scritti, in entrambi i casi conservando la loro identica funzione di sostitutivi di entità matematiche.
Nel caso della scelta di simboli-oggetto, si ha l'abaco nelle sue varie forme. Per rappresentare le unità semplici si usano oggetti-simbolo tutti uguali fra loro (per esempio i calculi) in quantità pari al numero massimo di unità ammissibile per ogni ordine (nove nel sistema decimale), oppure in quantità minore, se si conviene di assegnare ad alcuni di essi un valore diverso, come avviene nell'abaco a bottoni, ove il bottone superiore vale cinque bottoni inferiori, in altre parole cinque unità. La distinzione dei vari ordini di unità è affidata alla diversa posizione delle scanalature in seno all'abaco.
Se, invece, i simboli sono dei segni scritti, si ottiene un sistema di numerazione scritta. In particolare vogliamo mostrare il processo di evoluzione dall'abaco al sistema di numerazione scritta posizionale.
Si potrebbe pensare dapprima di usare al posto dei calculi dei Romani, usati per rappresentare con oggetti le unità semplici, dei simboli scritti. Questi devono essere diversi l'uno dall'altro e tanti quante sono le unità semplici, cioè nove nel sistema decimale. Tali simboli scritti sono detti "cifre". Dentro ciascuna scanalatura dell'abaco si potrebbe quindi porre la cifra che indica il numero di unità dell'ordine corrispondente alla scanalatura, sostituendo così i calculi (figura 12). Successivamente, si può pensare di eliminare anche le scanalature o colonne, e rappresentare i diversi ordini delle unità anch'essi con segni o simboli scritti. Utilizzando, per esempio, le attuali cifre, il numero 2.467 si potrebbe scrivere nel seguente modo:

1000 100 10 1
2 4 6 7

cioè ponendo sotto al simbolo di ciascun ordine (nel nostro caso 1, 10, 100 ecc.) la cifra che indica il numero di unità di quell'ordine che contribuisce alla formazione del numero in questione. Tale tipo di scrittura, che non è ancora posizionale ma semplicemente moltiplicativa, fu in uso fin da tempi antichissimi presso le popolazioni orientali (Cinesi).8
Essa non è altro che la trasposizione grafica dell'abaco: al posto delle scanalature ci sono le cifre 1, 10, 100 ecc. che indicano i vari ordini di unità, e al posto dei calculi ci sono le cifre che indicano le unità dei vari ordini. Il principio di economia suggerisce, poi, di evitare d'inventare e scrivere simboli diversi per indicare i vari ordini, che sono, fra l'altro, infiniti.
Tali simboli diventano superflui, e quindi possono essere soppressi, se si conviene di affidare alla posizione delle cifre, indicanti il numero di unità dei vari ordini, il compito di specificare l'ordine delle unità stesse. Si ha così il ben noto principio posizionale applicato alla numerazione scritta. È però necessario, a questo punto, introdurre un altro simbolo, lo zero, per indicare l'assenza di unità. In tal maniera, per rappresentare in forma scritta un numero, comunque grande esso sia, risultano sufficienti i simboli grafici (cifre) utlizzati per indicare le unità semplici e lo zero, vale a dire 10 cifre nel sistema decimale. È l'affermazione del principio di economia, che successivamente informerà di sé tutta la scienza moderna, trovando la sua massima espressione nel formalismo matematico, cui ricorrono sempre di più le scienze sperimentali e d'osservazione (astronomia).
È su tali osservazioni che dovette attuarsi un'importante modifica dell'abaco a bottoni degli antichi Romani, la quale consistette nel sostituire i calculi con un unico gettone posto al disopra di ciascuna scanalatura e portante impressa la cifra designante il numero di unità di quell'ordine rappresentato dai calculi prima presenti fisicamene entro le scanalature e ora soppressi. Il termine gettone deriva dal latino iacere, che significa gettare. Infatti, i calculi erano gettati entro le scanalature: il gettone sostituì così di nome e di fatto l'operazione del "gettare i calculi", soppressa nel nuovo abaco. Tali cifre9, impresse nei gettoni, furono chiamate apici o figure d'abaco per ovvi motivi, ed erano molto somiglianti alle cifre arabe (figura 12).
Questa variante dell'antico abaco romano fu attribuita, dalla tradizione, ai Neopitagorici della scuola alessandrina, il che spiega i nomi Mensa Pithagorica o Tavola Pitagorica o Arco Pitagorico con i quali fu battezzato il nuovo abaco a colonne, il cui significato era mutato profondamente, in quanto esso, oltre a fornire uno strumento per calcolare, consentiva ora di rappresentare un numero nel nuovo sistema posizionale per mezzo di numerali, a meno dello zero. Successivamente, furono aboliti i gettoni e le cifre furono scritte direttamente sopra le colonne. Dunque, fu sempre più manifesta l'identificazione concettuale di quest'ultimo tipo d'abaco con l'algoritmo o algorismo10, termine con cui inizialmente era chiamato il sistema di numerazione posizionale nei paesi latini, tant'è che i matematici italiani dei secoli XII e XIV usavano indifferentemente i due termini, abaco e algoritmo, per riferirsi al sistema numerico posizionale. Quest'ultimo rese obsoleto l'uso dell'abaco, che era giustificato principalmente dalle difficoltà di eseguire i calcoli con il vecchio sistema di numerazione additivo, risultando invece con esso più facili e rapidi. Infatti, il nuovo sistema di numerazione posizionale dava la possibilità sia di rappresentare i numeri con maggior economia di simboli, sia di semplificare i procedimenti del calcolo scritto, e pertanto vanificò il vantaggio dell'abaco, decretandone, almeno in Europa, la definitiva scomparsa. Con l'identificazione fra abaco e algoritmo si concluse la disputa fra abachisti e algoritmisti, vale a dire fra coloro che sostenevano i vantaggi del calcolare per mezzo dell'abaco oppure con il sistema di numerazione scritta.

Un errore di trascrizione
Verso la fine del primo libro dell'Ars Geometrica di Severino Boezio11  sono contenute la descrizione e le regole d'uso dell'abaco neopitagorico, il quale è menzionato proprio con il nome Mensa Pithagorica. Questo abaco, detto anche abaco di Boezio, ebbe particolare diffusione nelle scuole claustrali medievali, per opera del teologo e matematico francese Gerberto (950-1003 d.C.), divenuto papa col nome di Silvestro II nel 999.
Nel riprodurre successivamente il manoscritto dell'Ars Geometrica, il copista, per errore, sostituì l'abaco neopitagorico con la comune tavola di moltiplicazione, di aspetto assai simile, conservando però per quest'ultima il nome di Tavola Pitagorica12 , che, dunque, non deve il suo nome né a Pitagora né ad alcuno dei suoi seguaci, bensì soltanto a un errore di trascrizione.

Il quipu
Un sistema ingegnoso, quanto semplice ed economico, per rappresentare i numeri e far di conto, è quello utilizzato dagli Incas, popolazione precolombiana, il cui fiorente impero corrispondeva agli attuali territori del Perù, della Bolivia e dell'Ecuador. Questa grande civiltà, i cui inizi risalgono soltanto al secolo XII, pur non conoscendo né la ruota né la scrittura, almeno nel senso abituale del termine, mostra segni di alto livello culturale, come traspare, fra le altre cose, dall'ingegnoso metodo adottato per rappresentare i numeri e fare i calcoli. Il loro "abaco" era costituito da un sofisticato sistema di cordicelle a nodi, il quipu o quipo, che significa nodo. Esso assolveva altre molteplici funzioni, essendo utilizzato da specializzati funzionari dell'impero, i quipucamayocs o guardiani dei nodi (figura 13), anche per rappresentare eventi religiosi, come calendario, come registratore di rilevazioni statistiche, come delatore di messaggi. Il quipu era formato da una cordicella principale, lunga circa 60 cm, alla quale erano legate numerose altre cordicelle. Il sistema utilizzato era il decimale. Le unità semplici erano rappresentate con altrettanti nodi raggruppati in gruppi corrispondenti ai diversi ordini, unità semplici, decine, centinaia ecc. Tali gruppi erano opportunamente distanziati lungo la stessa cordicella (figura 14).

Il chimpu
Un sistema derivato dal quipu è tuttora usato dagli indios del Perù e della Bolivia. Lo strumento, a cordicelle e nodi, si chiama chimpu (figura 15). I vari ordini sono rappresentati da successive cordicelle: una singola cordicella corrisponde alle unità semplici, due cordicelle legate assieme corrispondono alle decine, tre cordicelle legate assieme corrispondono alle centinaia ecc. Le unità semplici sono rappresentate da altrettanti nodi. Pertanto 5 nodi su una singola cordicella rappresentano il numero cinque, 5 nodi su due cordicelle legate assieme rappresentano il numero cinquanta, 5 nodi su tre cordicelle legate assieme rappresentano il numero cinquecento e così via.

Il nepohualtzitzin
Recenti scavi archeologici hanno portato alla luce, nell'America centrale, l'abaco utilizato dagli Aztechi nei secoli X-XI, molto simile agli abachi cinese e giapponese, ma differente nel numero di palline situate nelle parti inferiore e superiore, 3 e 4 rispettivamente.

Lo Scoty
In Russia l'abaco, detto scoty o scet, ha la medesima struttura, ad aste o fili verticali e palline, degli abachi cinese e giapponese, con la differenza che su ogni filo ci sono dieci palline e non è diviso in due parti. Il sistema di numerazione rappresentato è il decimale e ogni filo è dedicato a un ordine di unità. Il numero di unità di ciascun ordine è ottenuto spostando verso il bordo superiore dell'abaco il corrispondente numero di palline. Per facilitare con un solo colpo d'occhio la lettura del numero di unità di ciascun ordine, le palline quinta e sesta sono di colore differente dalle altre.



Note:
1 Nel sistema di numerazione additivo, un numero è ottenuto per somma dei numeri indicati da opportuni simboli, i quali hanno il medesimo valore quale che sia la loro collocazione all'interno della rappresentazione dell'intero numero. In realtà il sistema dei Romani è un misto fra sistema additivo, sottrattivo e moltiplicativo, cioè è additivo in senso lato, in quanto sottrazioni e moltiplicazioni sono riconducibili a addizioni. Per esempio i Romani rappresentavano il numero 43 con il numerale XLIII, in cui i simboli X, L e I rappresentano rispettivamente dieci, cinquanta e uno. Nella prima parte del numerale è fatta la sottrazione fra cinquanta e dieci (XV), mentre nella seconda parte si somma tre volte l'unità (III). Inoltre, per rappresentare il numero novemila, per esempio, usavano il numerale IXM, che rappresenta il numero in questione come prodotto fra nove (IX) e mille (M). Altro carattere spurio del sistema di numerazione romano era costituito dalla base del sistema, che era duplice: dieci (base primaria) e cinque (base ausiliaria). Infatti, usavano numerali particolari per rappresentare raggruppamenti di unità in base cinque: V per cinque, L per cinquanta, D per cinquecento ecc. Inoltre, la parte frazionaria era a base dodici, poiché l'unità semplice, detta dai Romani axis, era divisa in dodici once. Il loro sistema era dunque additivo, decimale e quinario per la parte intera, duodecimale per la parte frazionaria.
2 Chabauillet, Catalogo n. 1898; Orioli, "Sopra uno specchio coi Dioscuri, e la gemma così detta calcolatoria esistente a Parigi", in Bullett. Istit., 1865, pp. 152-157.
3 Del Museo Capitolino, tomo IV, tav. 20, Fulgoni, Roma 1782.
4 Velseri, "Epistolae ad Viros Illustres", in Opera Omnia, Norimberga 1682, pp. 820-842.
5 Garrucci, "Notizia di una tavoletta calcolatoria romana", Bullettino Archeologico Napolitano, Nuova serie, anno II, Decembre 1853, pp. 93-96.
6 I numerali indicati sono quelli arcaici (cfr. figura 9).
7 La caratteristica fondamentale di un abaco è il numero di anelli o palline o più in generale di contatori che si trovano in ciascun filo delle due parti, solitamente superiore e inferiore, in cui è diviso l'abaco. Così si dice che lo swan-pan è un abaco 2/5, cioè ha su ogni filo due palline sopra e cinque palline sotto la linea orizzontale di separazione, mentre il soroban è un abaco 1/4 ecc.
8 G. Libri, Histoire des sciences mathematiques en Italie, 1, Paris 1838, pp. 202-203.
9 Non comprendevano ancora lo zero.
10 Il termine algoritmo deriva dalla latinizzazione di Al Khovarizmi, soprannome del matematico arabo Mohammed Ben Musa vissuto nel sec. IX, indicante la provincia persiana del Korassan da cui proveniva.
11 Risalente molto probabilmente, secondo le moderne indagini filologiche, al secolo XI e invece attribuita a Severino Boezio (480-526 d.C.), per il fatto che negli antichi manoscritti essa si trova assieme all'opera De Institutione Arithmetica, compilata dallo statista romano, come rifacimento dell'opera di Nicomaco di Gerasa Introduzione Aritmetica del I secolo d.C.
12 V. G. Enestrom in Bibliotheca Mathematica (2) 8 (1894), a pagina 120, e P.Tannery in L'Intermediaire des Mathematiciens 4(1897), nelle pagine 162-163, citano la sostituzione dell'abaco neopitagorico con la tavola di moltiplicazione.

Bibliografia
1. G. Ifrah, Storia universale dei numeri, Mondadori, Milano 1989.
2. R. Bombelli, Studi archeologico-critici circa l'antica numerazione italica, 1, Roma 1876.
3. V. G. Enestrom, Bibliotheca mathematica, (2) 8, anno 1894.
4. P. Tannery, L'Intermediaire des Mathematiciens, 4, anno 1897.
5. S. Boezio, De Institutione Arithmetica, Lipsia 1867. A cura di G. Friedlein.
6. M. Charles, Comptes Rendus hebdomadaires des Sciences de l'Academie des Sciences de Paris, 16, anno 1843; 17 anno 1843; 64 anno 1867.
7. B. Boncompagni, Bollettino di bibliografia e storia delle scienze matematiche, 10, anno 1877; 14 anno 1881.
8. E. Narducci, Bollettino di bibliografia e storia delle scienze matematiche, 15, anno 1882, 14

Siti di approfondimento:
htpp://www.ee.ryerson.ca:8080/ielf/abacus
htpp://www.show.it/china/abaco.htm
htpp://hawk.hama-med.ac.jp/dbk/abacus.html
htpp://www.cut-the-knot.com/blue/Abacus.html